第一二章笔记

机器学习三观

what：什么是机器学习？

研究关于"学习算法"（一类能从数据中学习出其背后潜在规律的算法）的一门学科

PS ：深度学习指的是神经网络那一类学习算法，因此是机器学习的子集

why：为什么要学习机器学习？

• 从事机器学习理论的研究
• 从事机器学习系统的开发
• 将机器学习中的算法迁移应用到自己的研究领域
• 从事 AI应用方向的研究：自然语言处理 (NLP) 、计算机视觉 (CV)推荐系统等

how：怎样学机器学习？

入门可以先学习西瓜书+南瓜书，后期根据自己的需求去钻研不同的书

一、绪论

1.引言

​ 西瓜书主要围绕着“西瓜”来讲的，整个书就是围绕着如何使用一系列学习算法训练一个模型来判别“好瓜”和“坏瓜”。这里就有两个概念：学习算法和模型。我们都知道当我们判断一个瓜熟没熟都会拍一拍它，如果发出“咚，咚”的清脆声，我们能确定这个瓜熟了，这是我们日常生活的经验，在机器学习中我们称为数据。那么如何通过这些数据得到一个模型来辨别一个瓜熟没熟呢。这个就需要算法来解决，我们的算法需要学习数据的特征规律，从而生成模型。那机器学习研究的就是：在计算机上从数据中产生”模型“的算法，也称为学习算法。模型就可以理解为函数，用来解决实际问题。

2.假设空间和版本空间

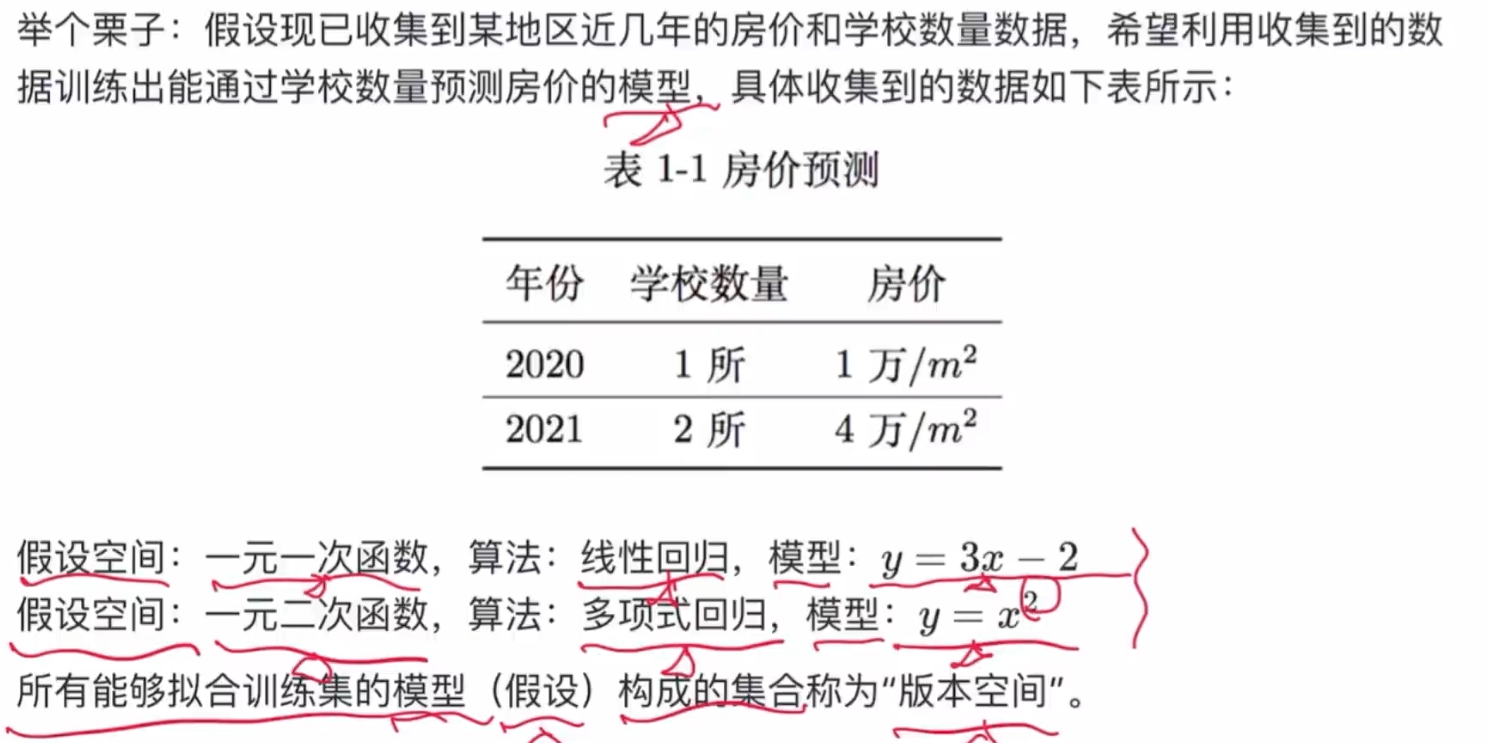
• 假设空间：

我们认为那些方法可以去预测（不管是否真的可以预测），它们的集合叫假设空间

• 版本空间：

所有能够拟合训练集的模型（假设）构成的集合称为”版本空间“

3.基本术语

在南瓜书中，总结的基本术语有：样本、样本空间、数据集、模型、标记、泛化和分布。

算法：

​ 从数据中学得"模型"的具体方法，例如线性回归、对数几率回归、决策树等。

模型：

​ "算法"产出的结果称为"模型"，通常是具体的函数或者可抽象地看作为函数，例如一元线性回归算法产出的模型即为形如$f(x)=wx+b$的一元一次函数。

样本：

​ 也称为“示例”，是关于一个事件或对象的描述。

例如，对西瓜的描述：

$x=（色泽：青绿；根蒂：蜷缩；敲响：浑浊）$

就是一个样本，其中的色泽是西瓜的一个属性，青绿是这个属性对应的一个属性值，通常我们会使用向量$\textbf{x}$来表示这些属性值也称为特征向量。

(向量中的元素用分号"；"分隔时表示此向量为列向量，用逗号"，"分隔时表示为行向量)

标记：

​ 机器学习的本质就是在学习样本在某个方面的表现是否存在潜在的规律，我们称该方面的信息为"标记"

​ 标记也称标签是对样本结果的一个“标记”，比如我们训练集中要给定这个瓜是好瓜还是坏瓜，就需要为这个瓜打上标签，一般我们标记分为两种，一种是离散型的，一种是连续型的。离散型的表示为 $\mathcal{Y}={0,1}$，连续型的表示为 $\mathcal{Y}=\R$。在机器学习中有标签的任务称为“监督学习”，无标签的任务称为“无监督学习”。

样本空间：

​ 在线性代数中向量所在的空间称为向量空间，那么样本中用来表示样本的特征向量所在的空间就称为样本空间也称属性空间。用$\mathcal{X}$表示

标记空间：

​ 标记所在的空间称为"标记空间"或"输出空间"，数学表示为花式大写的$Y$

分类

• 根据标记的取值类型不同，可将机器学习任务分为以下两类：

​ 1.当标记取值为离散型时，称此类任务为"分类"，例如学习西瓜是好瓜还是坏瓜、学习猫的图片是白猫还是黑猫等。

​ 1.1.当分类的类别只有两个时，称此类任务为“二分类“，通常称其中一个为"正类"，另一个为''反类"或"负类";当分类的类别超过两个时，称此类任务为"多分类"。

​ 1.2.由于标记也属于样本的一部分，通常也需要参与运算，因此也需要将其数值化，例如对于二分类任务，通常将正类记为 1 ，反类记为 0，即$Y$={ 0 , 1 }。这只是一般默认的做法，具体标记该如何数值化可根据具体机器学习算法进行相应地调整，例如第 6 章的支持向量机算法则采用的是$Y$={-1,+1}

​ 2.当标记取值为连续型时，称此类任务为"回归"，例如学习预测西瓜的成熟度、学习预测未来的房价等。由于是连续型，因此标记的所有可能取值无法直接罗列，通常只有取值范围，回归任务的标记取值范围通常是整个实数域 $R$ ，即$Y=R$

• 根据是否有用到标记信息，可将机器学习任务分为以下两类：

​ 1.模型训练阶段有用到标记信息时，称此类任务为"监督学习"

​ 2.在模型训练阶段没用到标记信息时，称此类任务为"无监督学习"

数据集：

​ 通常用来存储特征向量的集合称为数据集， $D={x_1,x_2,···,x_m}$表示含有$m$个样本的数据集。

泛化:

​ 由于机器学习的目标是根据已知来对未知做出尽可能准确的判断，因此对未知事物判断的准确与否才是衡量一个模型好坏的关键，我们称此为"泛化"能力。(即在测试集上的效果)

分布：

​ 此处的"分布"指的是概率论中的概率分布，通常假设样本空间服从一个未知"分布" D 而我们收集到的每个样本都是独立地从该分布中采样得到，即"独立同分布"。通常收集到的样本越多，越能从样本中反推出 1) 的佇自即越接近真相。

4.归纳偏好

在上一节“房价预测”的例子中，当选用一元线性回归算法时，学得的模型是一元一次函数，当选用多项式回归算法时，学得的模型是一元二次函数，所以不同的机器学习算法有不同的偏好，我们称为“归纳偏好”。

​ 对于不同的函数，哪一个更好，“奥卡姆剃刀”认为：“若多个假设和观察一致，则选择最简单的那个”。何为最简单，对于不同的函数哪一个的复杂度最低就说明它最简单。

是机器学习算法之间并没有优劣之分，只有是否适合解决当前问题的区分。在西瓜书中也证明了这一点：训练集之外的误差不会影响学习算法的期望值，对于任意的两个学习算法 ${\mathfrak{L}}{a}$和 ${\mathfrak{L}}{b}$始终都有：
$$
\sum\limitsfE{ote}({\mathfrak{L}}_{a}|X,f)=\sum\limitsfE{ote}({\mathfrak{L}}_{b}|X,f)
$$
这就是，“没有免费午餐定理”（No Free Lunch Theorem）简称NFL。

二、 模型评估与选择

1. 经验误差与过拟合

错误率：$E=\frac{a}{m}$，其中 m 为样本个数，a 为分类错误样本个数。

精度：精度 =1-错误率。

误差：学习器的实际预测输出与样本的真实输出之间的差异。

经验误差：学习器在训练集上的误差，又称为“训练误差”。

泛化误差：学习器在新样本上的误差。

2.评估方法

本节介绍了 3 种模型评估方法：留出法、交叉验证法、自助法。

留出法是对单一数据集划分的方法，它直接将数据集 $D$划分为两个互斥的集合，一个作为训练集 $S$一个作为测试集 $T$，在训练集上训练出模型后用测试机评估测试误差，作为对泛化误差的估计。但是由于训练集包含大多数的样本，训练出来的模型更接近用 $D$训练出的模型，所以这样测试的结果不够准确，反之测试相差较大。常见的作法是将大约 $2/3-4/5$的数据样本用于训练。

交叉验证法与留出法相似，它将数据集 $D$划分为 k$个互斥子集，通过分层采样得到每个子集 $D_i$，然后每次用 $k-1$个子集作为训练集，剩下的作为测试集，这样就可以进行 $k$次训练和测试，这种交叉验证法也被称为“k折交叉验证”。交叉验证法常用于对比同一算法的不同配置之间的效果。并且在交叉验证法中有个特例：留一法（Leave-One-Out，简称LOO），即当数据集有 $m$个样本$k=m$。这种方法的我缺点也很明显，当数据较大时，计算开销也是非常大的，而且估算的结果也未必有其他评估方法的准确，NFL定理可以证明这一点。

自助法是以自动采样法为基础的，给定包含$m$个样本的数据集$D$，我们对它进行采样，产生数据集$D$：每次随机从$D$中挑选一个样本，将其拷贝放入$D'$，然后再将该样本放回初始数据集$D$中；这个过程重复执行$m$次后，我们就得到了包含$m$个样本的数据集$D'$，这就是自助采样的结果。然而，自助法产生的数据集改变了初始数据集的分布，这会引入估计偏差。

在调参与最终模型中，参数一般指的是算法本身的一些参数也称超参数，参数模型不同学得模型的性能往往有显著差别。调参和算法选择没什么本质区别：对每种参数配置都训练出模型，然后把对应最好模型的参数作为结果。但是学习算法的很多参数是在实数范围内取值，所以要对每个参数选定一个范围和变化步长。为模型配置好相应的模型参数后，就可以对新样本做预测了。

在模型评估与选择中用于评估测试的数据集称为“验证集”。

3. 性能度量

​ 性能度量就是衡量模型泛化能力的评价标准。性能度量反映了任务需求，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果；这意味着模型的“好坏”是相对的，什么样的模型是好的，不仅取决于算法和数据，还决定于任务需求。

4.比较检验

​ 为什么要做比较检验？“西瓜书”在本节开篇的两段话已经交代原由。简单来说，从统计学的角度，取得的性能度量的值本质上仍是一个随机变量，因此并不能简单用比较大小来直接判定算法（或者模型）之间的优劣，而需要更置信的方法来进行判定。

5.偏差与方差

为了了解学习算法“为什么”具有这样的性能，我们通过“偏差-方差分解”来解释学习算法的泛化性能。这个方法试图将学习算法的期望泛化错误率进行拆解，对于回归任务，可以将泛化误差分解为偏差、方差和噪声之和。

• 偏差：衡量了模型的预测结果在多大程度上偏离了真实值。

$$
{\operatorname{bias}}^{2}\left( \mathbf{x} \right) = {\left( \bar{f}\left( \mathbf{x} \right) {-} y \right)}^{2}
$$

• 方差：衡量了模型的预测结果对训练数据的敏感程度。

$$
\operatorname{var}\left( \mathbf{x} \right) = {\mathbb{E}}_{D}\left\lbrack {\left( f\left( \mathbf{x};D \right) {-} \bar{f}\left( \mathbf{x} \right) \right)}^{2} \right\rbrack
$$

• 噪声：衡量了学习算法在学习任务上所能达到期望泛化的下界。

$$
{\varepsilon}^{2} = {\mathbb{E}}{D}\left\lbrack {\left( y{D} {-} y \right)}^{2} \right\rbrack
$$