动手学数据分析第三章模型搭建和评估

经过前面的两章的知识点的学习，我可以对数数据的本身进行处理，比如数据本身的增删查补，还可以做必要的清洗工作。

那么下面我们就要开始使用我们前面处理好的数据了。

这一章我们要做的就是使用数据，我们做数据分析的目的也就是，运用我们的数据以及结合我的业务来得到某些我们需要知道的结果。

那么分析的第一步就是建模，搭建一个预测模型或者其他模型；我们从这个模型的到结果之后，我们要分析我的模型是不是足够的可靠，那我就需要评估这个模型。

我们拥有的泰坦尼克号的数据集，那么我们这次的目的就是，完成泰坦尼克号存活预测这个任务。

介绍相关库

在进行搭建模型前,我们需要引入相关库

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import Image

pandas和numpy

pandas和numpy在前几章已经介绍了是数据处理的常用库,我们来介绍其他库

matplotlib.pyplot

Pyplot 是 Matplotlib 的子库，提供了和 MATLAB 类似的绘图 API。

Pyplot 是常用的绘图模块，能很方便让用户绘制 2D 图表。

Pyplot 包含一系列绘图函数的相关函数，每个函数会对当前的图像进行一些修改，例如：给图像加上标记，生新的图像，在图像中产生新的绘图区域等等。

seaborn

Seaborn 是基于 Python 且非常受欢迎的图形可视化库，在 Matplotlib 的基础上，进行了更高级的封装，使得作图更加方便快捷。即便是没有什么基础的人，也能通过极简的代码，做出具有分析价值而又十分美观的图形。

IPython.display

display 函数是 IPython 的一个内置函数，它用于在 Jupyter Notebook 环境中显示 Python 对象的图形化表示或其他格式化输出，例如图像、音频、视频、HTML 等。

display 函数可以接受一个或多个参数，每个参数都是一个 Python 对象。它会自动根据对象的类型选择合适的显示方式，并在 Jupyter Notebook 中显示出来。如果需要在同一个单元格中显示多个对象，可以在 display 函数中依次列出这些对象即可。

绘图设置

%matplotlib inline

是一个魔法函数（Magic Functions）。官方给出的定义是：IPython有一组预先定义好的所谓的魔法函数（Magic Functions），你可以通过命令行的语法形式来访问它们。可见“%matplotlib inline”就是模仿命令行来访问magic函数的在IPython中独有的形式。

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
plt.rcParams['figure.figsize'] = (10, 6)  # 设置输出图片大小

载入数据

# 读取原数据数集
train = pd.read_csv('train.csv')
train.shape

train.head()

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Ticket	Fare	Cabin	Embarked
0	1	0	3	Braund, Mr. Owen Harris	male	22.0	1	A/5 21171	7.2500	NaN	S
1	2	1	1	Cumings, Mrs. John Bradley (Florence Briggs Th…	female	38.0	1	PC 17599	71.2833	C85	C
2	3	1	3	Heikkinen, Miss. Laina	female	26.0	0	STON/O2. 3101282	7.9250	NaN	S
3	4	1	1	Futrelle, Mrs. Jacques Heath (Lily May Peel)	female	35.0	1	113803	53.1000	C123	S
4	5	0	3	Allen, Mr. William Henry	male	35.0	0	373450	8.0500	NaN	S

#读取清洗过的数据集
data = pd.read_csv('clear_data.csv')

	PassengerId	Pclass	Age	SibSp	Fare	Sex_female	Sex_male	Embarked_C	Embarked_S
0	0	3	22.0	1	7.2500	0	1	0	1
1	1	1	38.0	1	71.2833	1	0	1	0
2	2	3	26.0	0	7.9250	1	0	0	1
3	3	1	35.0	1	53.1000	1	0	0	1
4	4	3	35.0	0	8.0500	0	1	0	1

模型搭建

处理完前面的数据我们就得到建模数据，下一步是选择合适模型
在进行模型选择之前我们需要先知道数据集最终是进行监督学习还是无监督学习
模型的选择一方面是通过我们的任务来决定的。
除了根据我们任务来选择模型外，还可以根据数据样本量以及特征的稀疏性来决定
刚开始我们总是先尝试使用一个基本的模型来作为其baseline，进而再训练其他模型做对比，最终选择泛化能力或性能比较好的模型

这里的建模，并不是从零开始，自己一个人完成完成所有代码的编译。我们这里使用一个机器学习最常用的一个库（sklearn）来完成我们的模型的搭建

下面给出sklearn的算法选择路径，供大家参考

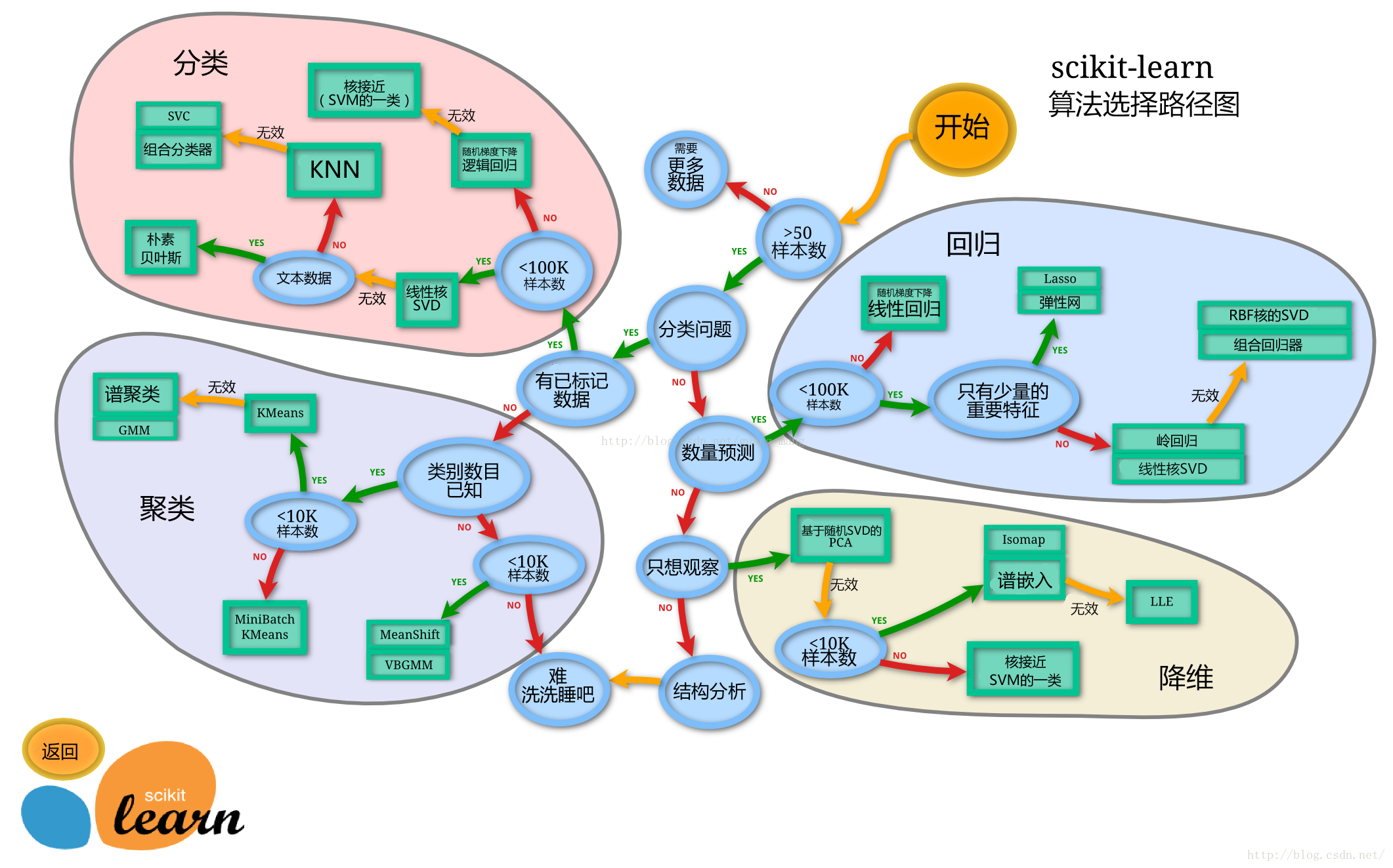
任务一：切割训练集和测试集

这里使用留出法划分数据集

将数据集分为自变量和因变量
按比例切割训练集和测试集(一般测试集的比例有30%、25%、20%、15%和10%)
使用分层抽样
设置随机种子以便结果能复现

train_test_split

sklearn中切割数据集的方法为train_test_split

官方wiki

sklearn.model_selection.train_test_split(*arrays, test_size=None, train_size=None, random_state=None, shuffle=True, stratify=None)

test_size：float or int, default=None

测试集的大小，如果是小数的话，值在（0,1）之间，表示测试集所占有的比例；

如果是整数，表示的是测试集的具体样本数；

如果train_size也是None的话，会有一个默认值0.25

train_size：float or int, default=None

和test_size一样，同上

random_state：int or RandomState instance, default=None

(只有当shuffle=True时,此参数才有作用)

这个参数表示随机状态的种子，因为每次分割都是随机的,但如果给定一个固定种子,划分的结果是相同的

shuffle: bool, default=True

是否随机打乱顺序后再划分数据,默认是要打乱的

# 一般先取出X和y后再切割，有些情况会使用到未切割的，这时候X和y就可以用,x是清洗好的数据，y是我们要预测的存活数据'Survived'
X = data
y = train['Survived']

# 对数据集进行切割
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)
# 查看数据形状
X_train.shape, X_test.shape

任务二：模型创建

创建基于线性模型的分类模型（逻辑回归）
创建基于树的分类模型（决策树、随机森林）
分别使用这些模型进行训练，分别的到训练集和测试集的得分
查看模型的参数，并更改参数值，观察模型变化

提示

逻辑回归不是回归模型而是分类模型，不要与LinearRegression混淆
随机森林其实是决策树集成为了降低决策树过拟合的情况
线性模型所在的模块为sklearn.linear_model
树模型所在的模块为sklearn.ensemble

#导入模块
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier

LogisticRegression()- 逻辑回归分类器(又叫logit回归，最大熵分类器)

官方wiki说明

部分参数说明如下：

penalty：惩罚项，str类型，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1G规范假设的是模型的参数满足拉普拉斯分布，L2假设的模型参数满足高斯分布，所谓的范式就是加上对参数的约束，使得模型更不会过拟合(overfit)，但是如果要说是不是加了约束就会好，这个没有人能回答，只能说，加约束的情况下，理论上应该可以获得泛化能力更强的结果。
dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。
c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。
fit_intercept：是否存在截距或偏差，bool类型，默认为True。
intercept_scaling：仅在正则化项为”liblinear”，且fit_intercept设置为True时有用。float类型，默认为1。

# 默认参数逻辑回归模型
lr = LogisticRegression()
lr.fit(X_train, y_train)

# 查看训练集和测试集score值
print("Training set score: {:.2f}".format(lr.score(X_train, y_train)))
print("Testing set score: {:.2f}".format(lr.score(X_test, y_test)))

# 调整参数后的逻辑回归模型
lr2 = LogisticRegression(C=100)
lr2.fit(X_train, y_train)

print("Training set score: {:.2f}".format(lr2.score(X_train, y_train)))
print("Testing set score: {:.2f}".format(lr2.score(X_test, y_test)))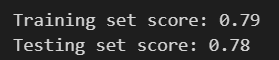

RandomForestClassifier()-随机森林

官方wiki

参数	作用
criterion	不纯度的衡量指标，有基尼系数和信息增益两种
max_depth	树的最大深度
min_samples_leaf	一个节点分支后，子节点必须最少包含的样本数，如果不能满足条件将不能发生分支
min_samples_split	一个节点如果要发生分支操作，必须要包含的最小样本数，不满足则不能分支
max_features	限制分支时考虑的特征个数
min_impurity_decrease	限制信息增益的减小，信息增益小于限定值时不发生分支

# 默认参数的随机森林分类模型
rfc = RandomForestClassifier()
rfc.fit(X_train, y_train)

print("Training set score: {:.2f}".format(rfc.score(X_train, y_train)))
print("Testing set score: {:.2f}".format(rfc.score(X_test, y_test)))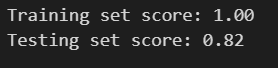

# 调整参数后的随机森林分类模型
rfc2 = RandomForestClassifier(n_estimators=100, max_depth=5)
rfc2.fit(X_train, y_train)

print("Training set score: {:.2f}".format(rfc2.score(X_train, y_train)))
print("Testing set score: {:.2f}".format(rfc2.score(X_test, y_test)))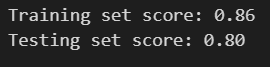

任务三：输出模型预测结果

输出模型预测分类标签
输出不同分类标签的预测概率

predict()-输出预测标签

官方wiki

参数：

X：array-like或sp matrix，shape = [n_samples, n_features]，测试样本，其中n_samples表示样本的数量，n_features表示特征的数量。
batch_size：整数，可选参数，指定每次迭代时处理的样本数量，默认值为None，表示一次性处理所有的样本。
verbose：整数，可选参数，控制输出信息的级别，默认值为0，表示不输出任何信息。
steps：整数，可选参数，指定每次迭代的步数，默认值为None，表示使用所有的步数。

# 预测标签
pred = lr.predict(X_train)
# 此时我们可以看到0和1的数组
pred[:10]

array([0, 1, 1, 1, 0, 0, 1, 0, 1, 1])

predict_proba-输出标签概率

官方wiki

输入:待预测的数据
输出:数组形式为(样本个数，样本类别数)，每一行代表某个样本在各个类上的概率，其和为1.

# 预测标签概率
pred_proba = lr.predict_proba(X_train)
pred_proba[:10]

array([[0.60870022, 0.39129978],
       [0.17725433, 0.82274567],
       [0.40750365, 0.59249635],
       [0.18925851, 0.81074149],
       [0.87973912, 0.12026088],
       [0.91374559, 0.08625441],
       [0.13293198, 0.86706802],
       [0.90560801, 0.09439199],
       [0.05283987, 0.94716013],
       [0.10936016, 0.89063984]])

模型评价

任务：加载数据并分割测试集和训练集

from sklearn.model_selection import train_test_split

train_test_split

sklearn中切割数据集的方法为train_test_split

官方wiki

之前有介绍故跳过

#读取训练和测试集作为xy
data = pd.read_csv('clear_data.csv')
train = pd.read_csv('train.csv')
X = data
y = train['Survived']

# 对数据集进行切割
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, random_state=0)

# 默认参数逻辑回归模型
lr = LogisticRegression()
lr.fit(X_train, y_train)

模型评估

模型评估是为了知道模型的泛化能力。
交叉验证（cross-validation）是一种评估泛化性能的统计学方法，它比单次划分训练集和测试集的方法更加稳定、全面。
在交叉验证中，数据被多次划分，并且需要训练多个模型。
最常用的交叉验证是 k 折交叉验证（k-fold cross-validation），其中 k 是由用户指定的数字，通常取 5 或 10。
准确率（precision）度量的是被预测为正例的样本中有多少是真正的正例
召回率（recall）度量的是正类样本中有多少被预测为正类
f-分数是准确率与召回率的调和平均

任务一：交叉验证

用10折交叉验证来评估之前的逻辑回归模型
计算交叉验证精度的平均值

sklearn.model_selection

交叉验证在sklearn中的模块为sklearn.model_selection

找了一个大佬的图,方便大家理解这个模块里都有什么(原出处)

也可以去官方wiki查看

1.Splitter Classes（分组）

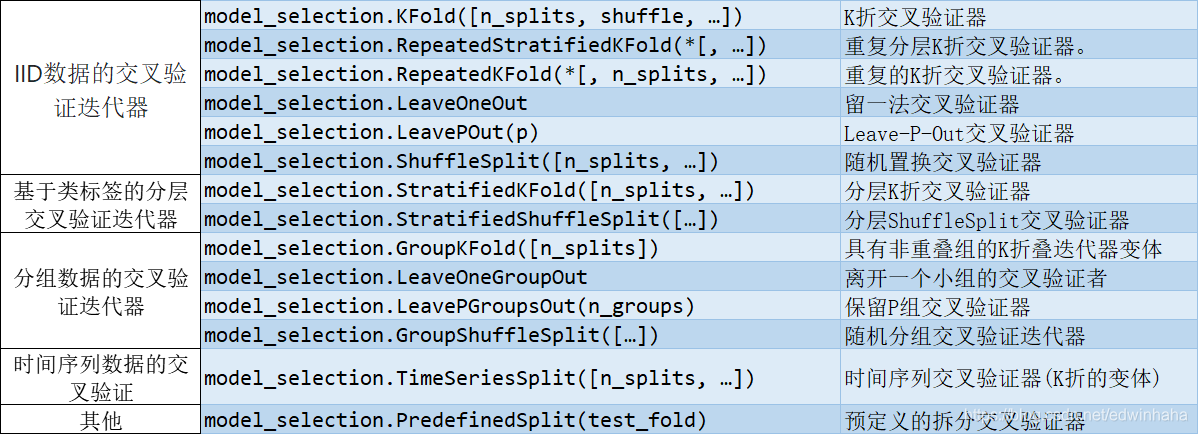
2.Splitter Functions（拆分训练集与测试集）

3.Hyper-parameter optimizers（超参数优化）

某些模型可以为某个参数的某个值范围拟合数据，其效率几乎与为一个参数的单个值拟合估算值的效率相同。可以利用此功能来执行更有效的交叉验证，以用于此参数的模型选择。

4.Model validation（模型验证）

5. 验证曲线：绘制分数来评价模型

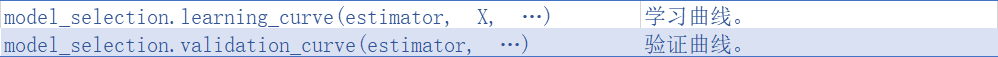
于是我们先引入模块

from sklearn.model_selection import cross_val_score

lr = LogisticRegression(C=100)
scores = cross_val_score(lr, X_train, y_train, cv=10)

LogisticRegression()逻辑回归

官方wiki

部分参数介绍:

dual:布尔，默认值=False*

对偶（约束）或原始（正则化，另见此等式）公式。双重配方仅针对 L2 惩罚使用 Liblinear 求解器实现。当 n_samples > n_features。

tol:float，默认值=1e-4*

停止标准的公差。

C: float，默认值 = 1.0*

正则化强度的倒数;必须为正浮点数。与支持向量机一样，较小的值表示更强正规化。

fit_intercept: bool，默认值=True*

指定常量（也称为偏置或截距）是否应为添加到决策函数中。

intercept_scaling: float，默认值 = 1*

仅在使用求解器“liblinear”时才有用 self.fit_intercept设置为 True。在本例中，x 变为 [x， self.intercept_scaling]，即具有恒定值等于 intercept_scaling 将追加到实例向量中。截距变为。intercept_scaling * synthetic_feature_weight

cross_val_score() 通过交叉验证评估分数

官方wiki

部分参数介绍:

estimator：estimator object implementing ‘fit’*

我们的算法模型

X：array-like of shape (n_samples, n_features)*

*y：array-like of shape (n_samples,) or (n_samples, n_outputs), default=None

我们的数据集

cv：int, cross-validation generator or an iterable, default=None*

我们要进行的交叉验证的方法

查看k折交叉验证分数

scores

array([0.80597015, 0.74626866, 0.74626866, 0.80597015, 0.88059701,
       0.8358209 , 0.74626866, 0.8358209 , 0.74242424, 0.72727273])

求一下平均交叉验证分数

print("Average cross-validation score: {:.2f}".format(scores.mean()))

Average cross-validation score: 0.80

任务二：混淆矩阵

计算二分类问题的混淆矩阵
计算精确率、召回率以及f-分数

混淆矩阵（Confusion Matrix）

在机器学习领域，混淆矩阵（Confusion Matrix），又称为可能性矩阵或错误矩阵。混淆矩阵是可视化工具，特别用于监督学习，在无监督学习一般叫做匹配矩阵。在图像精度评价中，主要用于比较分类结果和实际测得值，可以把分类结果的精度显示在一个混淆矩阵里面。

混淆矩阵的结构一般如下图表示的方法。

混淆矩阵要表达的含义：

混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；
每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目；每一列中的数值表示真实数据被预测为该类的数目。

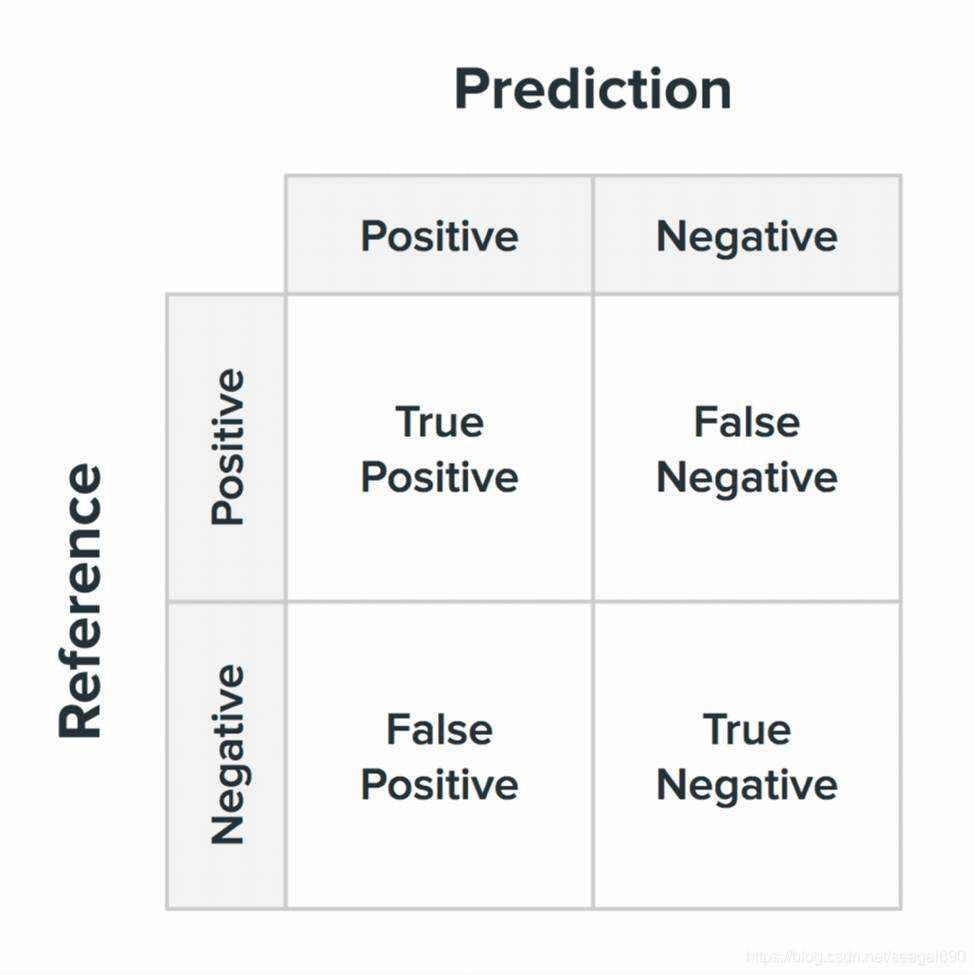
True Positive（TP）：真正类。样本的真实类别是正类，并且模型识别的结果也是正类。
False Negative（FN）：假负类。样本的真实类别是正类，但是模型将其识别为负类。
False Positive（FP）：假正类。样本的真实类别是负类，但是模型将其识别为正类。
True Negative（TN）：真负类。样本的真实类别是负类，并且模型将其识别为负类。该矩阵可用于易于理解的二类分类问题，但通过向混淆矩阵添加更多行和列，可轻松应用于具有3个或更多类值的问题。

从混淆矩阵得到分类指标

从混淆矩阵当中，可以得到更高级的分类指标：Accuracy（精确率），Precision（正确率或者准确率），Recall（召回率），Specificity（特异性），Sensitivity（灵敏度）。

计算方法

对于二分类问题，可以将样例根据其真实类别与机器学习器预测类别的组合划分为：

样例总数 = TP + FP + TN + FN。

则可以计算指标：总样例数=TP+FP+TN+FN

精确率（Accuracy）：

精确率是最常用的分类性能指标。可以用来表示模型的精度，即模型识别正确的个数/样本的总个数。一般情况下，模型的精度越高，说明模型的效果越好。

$$
Accuracy = \frac{TP+TN}{TP+FN+FP+TN}
$$

正确率或者准确率（Precision）：

又称为查准率，表示在模型识别为正类的样本中，真正为正类的样本所占的比例。一般情况下，查准率越高，说明模型的效果越好。

$$
Precision = \frac{TP}{TP+FP}
$$

召回率（Recall）：

又称为查全率，召回率表现出在实际正样本中，分类器能预测出多少。

Recall（召回率） = Sensitivity（敏感指标，True Positive Rate，TPR）= 查全率

表示的是，模型正确识别出为正类的样本的数量占总的正类样本数量的比值。一般情况下，Recall越高，说明有更多的正类样本被模型预测正确，模型的效果越好。

$$
Recall（召回率） = \frac{TP}{TP+FP}\
=Sensitivity（敏感指标，True Positive Rate，TPR）\
= 查全率
$$
查准率和查全率是一对矛盾的指标。一般来说，查准率高时，查全率旺旺偏低；二查全率高时，查准率往往偏低。

需要使用的模块和方法

混淆矩阵的方法在sklearn中的sklearn.metrics模块
混淆矩阵需要输入真实标签和预测标签
精确率、召回率以及f-分数可使用classification_report模块

from sklearn.metrics import confusion_matrix

# 训练模型
lr = LogisticRegression(C=100)
lr.fit(X_train, y_train)

# 模型预测结果
pred = lr.predict(X_train)

# 混淆矩阵
confusion_matrix(y_train, pred)

array([[354, 58],

[ 83, 173]], dtype=int64)

from sklearn.metrics import classification_report

# 精确率、召回率以及f1-score
print(classification_report(y_train, pred))

              precision    recall  f1-score   support

           0       0.81      0.86      0.83       412
           1       0.75      0.68      0.71       256

    accuracy                           0.79       668
   macro avg       0.78      0.77      0.77       668
weighted avg       0.79      0.79      0.79       668

任务三：ROC曲线

绘制ROC曲线
ROC曲线在sklearn中的模块为sklearn.metrics
ROC曲线下面所包围的面积越大越好

from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_test, lr.decision_function(X_test))
plt.plot(fpr, tpr, label="ROC Curve")
plt.xlabel("FPR")
plt.ylabel("TPR (recall)")
# 找到最接近于0的阈值
close_zero = np.argmin(np.abs(thresholds))
plt.plot(fpr[close_zero], tpr[close_zero], 'o', markersize=10, label="threshold zero", fillstyle="none", c='k', mew=2)
plt.legend(loc=4)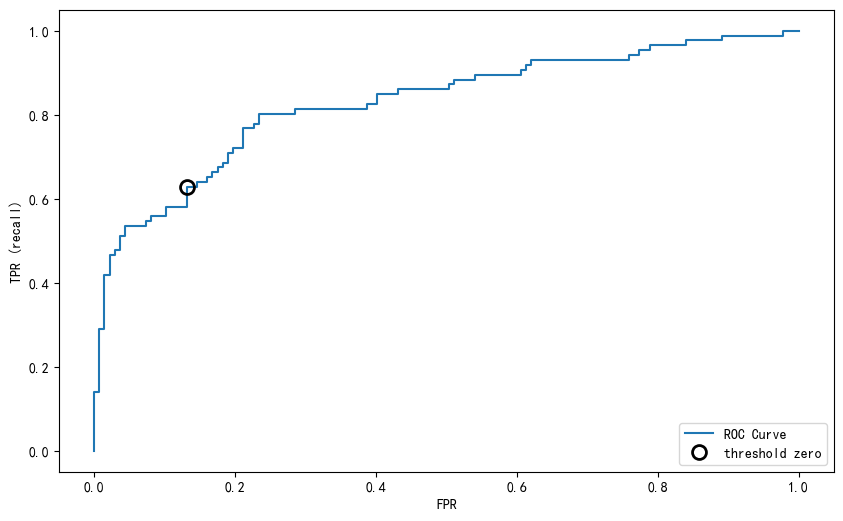

MSTG Blog

介绍相关库

pandas和numpy

matplotlib.pyplot

seaborn

IPython.display

绘图设置

载入数据

模型搭建

任务一：切割训练集和测试集

train_test_split

任务二：模型创建

提示

LogisticRegression()- 逻辑回归分类器(又叫logit回归，最大熵分类器)

RandomForestClassifier()-随机森林

任务三：输出模型预测结果

predict()-输出预测标签

predict_proba-输出标签概率

模型评价

任务：加载数据并分割测试集和训练集

train_test_split

模型评估

任务一：交叉验证

sklearn.model_selection

1.Splitter Classes（分组）

2.Splitter Functions（拆分训练集与测试集）

3.Hyper-parameter optimizers（超参数优化）

4.Model validation（模型验证）

5. 验证曲线：绘制分数来评价模型

于是我们先引入模块

LogisticRegression()逻辑回归

cross_val_score() 通过交叉验证评估分数

查看k折交叉验证分数

求一下平均交叉验证分数

任务二：混淆矩阵

混淆矩阵（Confusion Matrix）

从混淆矩阵得到分类指标

计算方法

精确率（Accuracy）：

正确率或者准确率（Precision）：

召回率（Recall）：

需要使用的模块和方法

任务三：ROC曲线

Docker学习(10)-Kubeadm方式部署Kubernetes(K8s)集群1.27.0版本

书生·浦语大模型 实战营(第二期)–第一节 书生·浦语大模型全链路开源体系

Comments NOTHING

取消回复

书生·浦语大模型实战营(第二期)–第一节书生·浦语大模型全链路开源体系